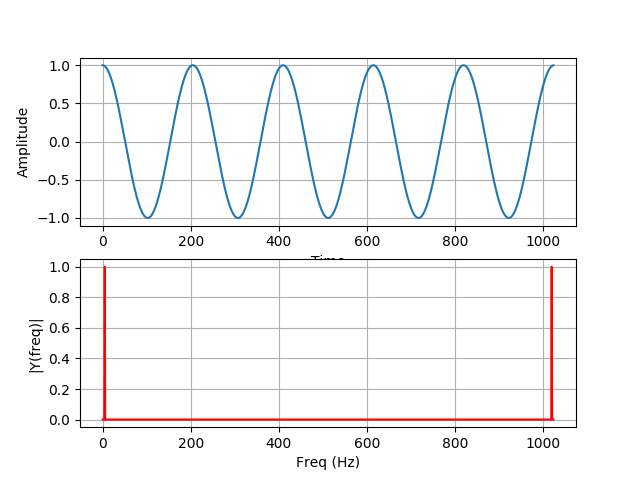
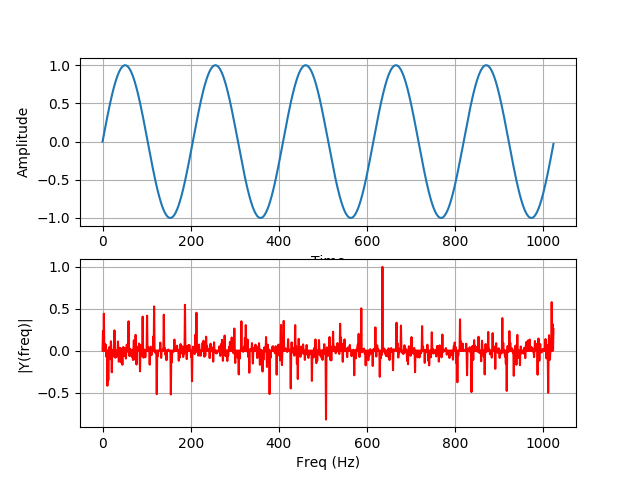
I wrote the cufft sample code and tested it.
Test results using cos () seem to work well, but using sin () results in incorrect results.
Below is my code. And attachment is result.
#include <iostream>
#include <fstream>
#include <sstream>
#include <stdio.h>
#include <chrono>
#include "cufft.h"
#include "cuda_runtime.h"
#include <stdlib.h>
#include <vector>
using namespace std;
/*
* Create N fake samplings along the function cos(x). These samplings will be
* stored as single-precision floating-point values.
*/
void generate_fake_samples(int N, float **out)
{
int i;
float *result = (float *)malloc(sizeof(float) * N);
double delta = 2 * M_PI * 5; // 5 = frequency
double delta1 = 2 * M_PI * 10; // 10 = frequency
printf("delta = %f\n", delta);
std::ofstream fout;
fout.open("../signal_data.txt");
for (i = 0; i < N; i++)
{
result[i] = sin(i * delta * 1/N); // + cos(i * delta1 * 1/N) + sin(i * delta1*2 * 1/N);
fout << result[i];
fout << "\n";
}
fout.close();
*out = result;
}
/*
* Convert a real-valued vector r of length Nto a complex-valued vector.
*/
void real_to_complex(float *r, cufftComplex **complx, int N)
{
(*complx) = (cufftComplex *)malloc(sizeof(cufftComplex) * N);
for (int i = 0; i < N; i++)
{
(*complx)[i].x = r[i];
(*complx)[i].y = 0;
}
}
int main(int argc, char *argv[])
{
int N = 1024; // Input Array Size
int BATCH = 1;
// int resultSize = (N/2 + 1) * BATCH; // FFT Result Size at 1-D FFT, Real-to-Complex
int resultSize = N * BATCH; // FFT Result Size at 1-D FFT, Complex-to-Complex
float * samples;
cufftHandle plan;
cufftComplex *inPtr;
cufftComplex *complexSamples, *devPtr, *results;
/* source data creation & Host memory allocation */
generate_fake_samples(N, &samples);
real_to_complex(samples, &complexSamples, N);
results = (cufftComplex *) malloc(sizeof(cufftComplex) * resultSize);
/* GPU memory allocation */
cudaMalloc((void **)&inPtr, sizeof(cufftComplex) * N * BATCH);
cudaMalloc((void **)&devPtr, sizeof(cufftComplex) * resultSize);
/* transfer to GPU memory */
cudaMemcpy(inPtr, complexSamples, sizeof(cufftComplex) * N * BATCH, cudaMemcpyHostToDevice);
/* creates 1D FFT plan */
cufftPlan1d(&plan, N, CUFFT_C2C, BATCH);
/* executes FFT processes */
cufftExecC2C(plan, inPtr, devPtr, CUFFT_FORWARD);
/* executes FFT processes (inverse transformation) */
// cufftExecC2R(plan, devPtr, inPtr);
/* transfer results from GPU memory */
cudaMemcpy(results, devPtr, sizeof(cufftComplex) * resultSize, cudaMemcpyDeviceToHost);
/* deletes CUFFT plan */
cufftDestroy(plan);
/* frees GPU memory */
cudaFree(devPtr);
printf("Fourier Coefficients:\n");
float maximum = 0.0f;
for (int i = 0; i < resultSize; i++)
{
if (fabs(results[i].x) > maximum)
{
maximum = fabs(results[i].x);
}
}
std::ofstream fout;
fout.open("../fft_data.txt");
for (int i = 0; i < resultSize; i++)
{
printf(" %d: (%2.4f, %2.4f)\n", i + 1, results[i].x / maximum,
results[i].y / maximum);
float temp = results[i].x / maximum;
fout << temp;
fout << "\n";
}
fout.close();
printf(" ...\n");
free(samples);
free(results);
return 0;
}