How to include the multiple heat sources in constraints

Physics Simulation Modulus Physics-ML Model Framework Technical Support (Modulus Only)
1

Dear Developer,

First of all, thank you very much for providing Modulus-sym! I have encountered a problem that I am unable to solve on my own, and I would like to seek your advice as well as insights from friends on the forum:

I have studied several examples in the tutorials, and I noticed that they all involve only a single heat source. In such cases, the heat flux density or heat flow can be converted into a temperature gradient on the heat source surface using Fourier’s law of heat conduction. However, my model involves multiple surface heat sources. Since each heat source is influenced by the others, the heat flux passing through each surface heat source is unknown. As a result, I am unable to calculate the temperature gradient for each heat source surface. I only know the original heat flux density for each individual heat source. In this situation, where multiple heat sources are coupled, how should I handle the heat sources? In what form should they be included in the constraints?

I would greatly appreciate your and the community’s feedback. Thank you in advance!

2

Hello, I write this code to create multiple heat source.

import numpy as np
from sympy import Symbol, exp, pi
import torch
import sys

import modulus.sym
from modulus.sym.hydra import ModulusConfig, instantiate_arch
from modulus.sym.solver import Solver
from modulus.sym.domain import Domain
from modulus.sym.geometry.primitives_2d import Rectangle
from modulus.sym.domain.constraint import (
    PointwiseBoundaryConstraint,
    PointwiseInteriorConstraint,
)

from modulus.sym.eq.pdes.diffusion import Diffusion
from modulus.sym.domain.validator import PointwiseValidator
from modulus.sym.key import Key
from modulus.sym.models.fully_connected import FullyConnectedArch

@modulus.sym.main(config_path="/content/", config_name="config_heat.yaml")
def run(cfg: ModulusConfig) -> None:

    # symbols
    x, y, t_symbol = Symbol("x"), Symbol("y"), Symbol("t")

    # parameters
    sigma = 0.1
    init_temp = 37 
    t_max = 10

    # heat source centers
    centers = [
    (-0.8, 0.8),
    (-0.8, -0.8),
    (0.8, 0.8),
    (0.8, -0.8)
    ]

    # heat_source
    heat_source_expr = sum(
        (1 / (2 * pi * sigma**2)) * exp(-((x - xi) ** 2 + (y - yi) ** 2) / (2 * sigma ** 2)) for xi, yi in centers)

    # diffusion equation with heat source
    diffusion_eq = Diffusion(T="T", D=0.1, Q=heat_source_expr, dim=2, time=True)

    # neural network
    heat_net = instantiate_arch(
        input_keys=[Key("x"), Key("y"), Key("t")],
        output_keys=[Key("T")],
        cfg=cfg.arch.fully_connected)

    # create nodes
    nodes = diffusion_eq.make_nodes() + [heat_net.make_node(name="heat_network")]

    # geometry and domain
    geo = Rectangle((-1.0, -1.0), (1.0, 1.0))
    domain = Domain()
    time_range = {t_symbol: (0, T_MAX)}

    # IC
    IC = PointwiseInteriorConstraint(
        nodes=nodes,
        geometry=geo,
        outvar={"T": init_temp}, # init temp, 37
        batch_size=cfg.batch_size.IC,
        parameterization={t_symbol: 0.0} # t=0
    )
    domain.add_constraint(IC, "IC")

    # BC
    BC = PointwiseBoundaryConstraint(
        nodes=nodes,
        geometry=geo,
        outvar={"T": init_temp}, # boundary temp, 37
        batch_size=cfg.batch_size.BC,
        parameterization=time_range, # includes all time
    )
    domain.add_constraint(BC, "BC")

    # interior constraint enforcing PDE residuals
    interior = PointwiseInteriorConstraint(
        nodes=nodes,
        geometry=geo,
        outvar={"diffusion_T": 0},  # Enforce PDE residuals
        batch_size=cfg.batch_size.interior,
        parameterization=time_range
    )
    domain.add_constraint(interior, "interior")

    # solver
    slv = Solver(cfg, domain)
    slv.solve()

if __name__ == "__main__":
    if 'google.colab' in sys.modules or 'ipykernel' in sys.modules:
        sys.argv = sys.argv[:1]

    run()

In this code, I defined my initial and boundary conditions as 37 Degree. I have used Gaussian 2D as heat source and I defined 4 different centers.
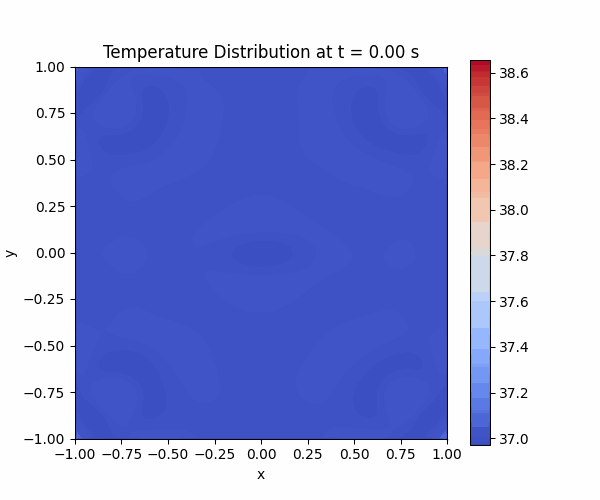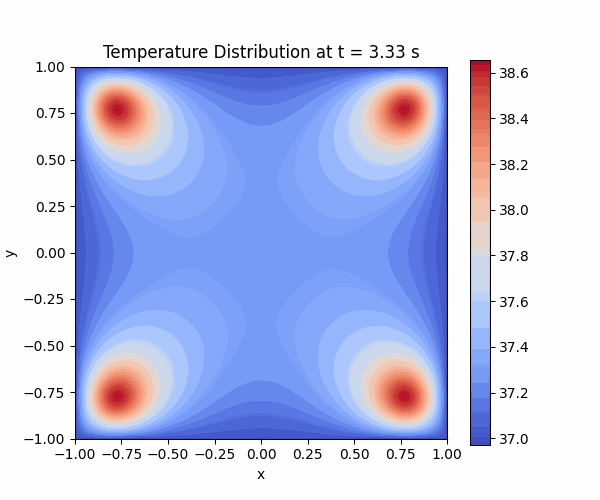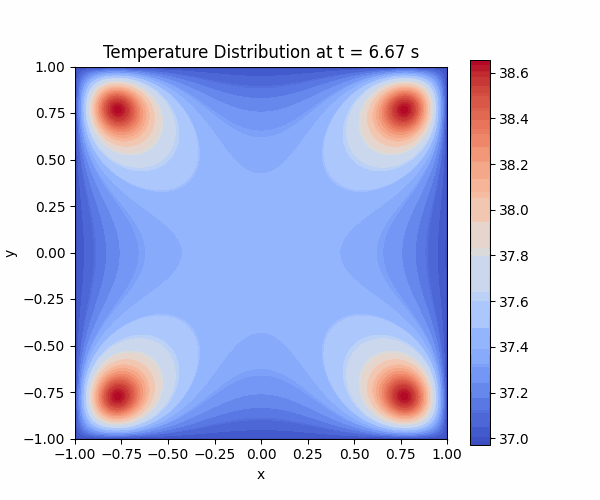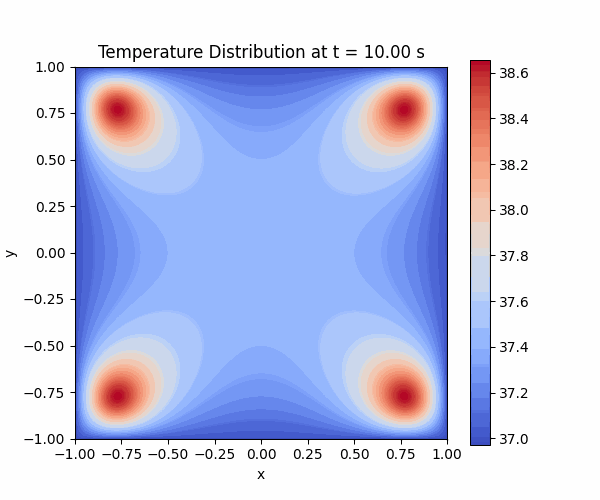
heat_equation2

And I get this result. I hope it helps for your case.