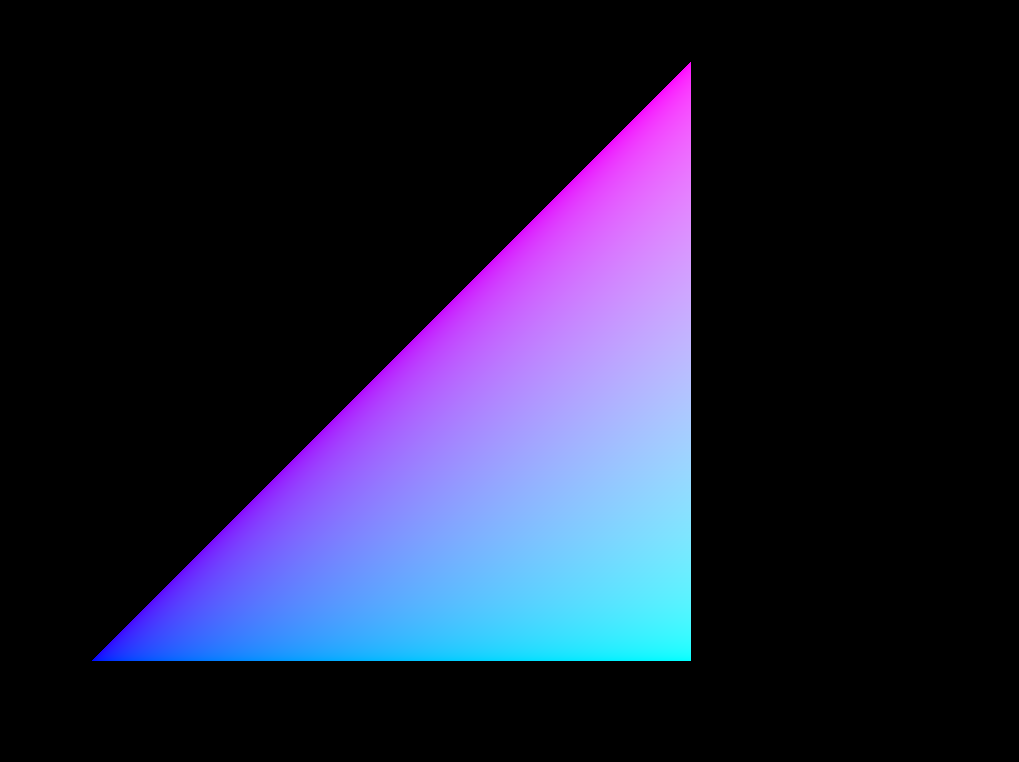
Yep, you’re definitely hitting the limits of single precision floats here.
Thanks for the optixTriangle reproducer!
So probably the way to think about this is that the scale of your triangle is around 85, because that’s the longest edge length. And your z-distance to the triangle is slightly over 1e-6. Single precision floats have about 7-8 decimal digits of accuracy, and the ratio of your triangle edge length to the expected t value is just less than ~1e8 (85/1e-6), which requires ~8 decimal digits of precision. This means that the intersector is finding the rounded hitT value to be <= 0 sometimes, and then returning a miss.
BTW, the hitT value reported doesn’t actually tell you what the intersector thinks it should be. In this case, the expected hitT value is:
0.00000116397814054 / 0.685875117779 = .00000169707007933046
The problem is just that this dips below the limits of single precision and sometimes gets rounded to zero or negative, resulting in a miss.
I expanded on your diff a little bit in order to visualize the precision:
static __forceinline__ __device__ void computeRay( uint3 idx, uint3 dim, float3& origin, float3& direction )
{
origin = make_float3(__uint_as_float(0x41f68678) + float(int(idx.x) - 400)*0.1f, __uint_as_float(0x41ed0423) + float(int(idx.y) - 400)*0.1f, __uint_as_float(0x359c39fc));
direction = make_float3(__uint_as_float(0x3f366880), __uint_as_float(0x3e177236), __uint_as_float(0xbf2f9583));
}
This puts your original ray at the image coordinate (400, 400), but allows us to see the whole triangle, and discover there are many misses across the triangle. Take special note that the lower left corner is much better than upper right. This is because the lower left corner is near the world space origin, and precision is higher there. Floating point precision gets worse further from the origin, so the upper right is worse than lower right.
If we add a small offset to the ray origin to give ourselves 1 extra decimal digit of precision (about 3 more bits), we can eliminate the misses:
static __forceinline__ __device__ void computeRay( uint3 idx, uint3 dim, float3& origin, float3& direction )
{
origin = make_float3(__uint_as_float(0x41f68678) + float(int(idx.x) - 400)*0.1f, __uint_as_float(0x41ed0423) + float(int(idx.y) - 400)*0.1f, __uint_as_float(0x359c39fc));
origin.z += 0.00001f;
direction = make_float3(__uint_as_float(0x3f366880), __uint_as_float(0x3e177236), __uint_as_float(0xbf2f9583));
}
Also be aware that ray direction affects precision, the linear solver will of course need to use the ray direction somewhere, likely in the form of a multiply, which may eat away at the number of bits of precision you have. This is all inherent in single precision floats, and you’ll get the same behavior if you use a software intersector under the same design constraints. If I ensure that multiplying by the ray direction doesn’t affect precision, we can see better results than the diagonal ray. This doesn’t help you, I just wanted to point out there are multiple sources of precision loss.
static __forceinline__ __device__ void computeRay( uint3 idx, uint3 dim, float3& origin, float3& direction )
{
origin = make_float3(__uint_as_float(0x41f68678) + float(int(idx.x) - 400)*0.1f, __uint_as_float(0x41ed0423) + float(int(idx.y) - 400)*0.1f, __uint_as_float(0x359c39fc));
direction = make_float3(0,0,-1);
}
I hope that helps. So yeah rays that get very close are subject to numeric precision noise. Would adding a safety margin distance away from the cube walls be a viable workaround for your simulation?
–
David.